Research Article - Onkologia i Radioterapia ( 2023) Volume 17, Issue 2
Prostate cancer and cardiovascular disease: Correlated?
Shipra Banik1, Mahashweta Das2, Ishita Saha3, Rui Gong4, Poonam Singh5, Jinseog Kim6 and Rabindra Nath Das7*2Department of History, The University of Burdwan, Burdwan, West Bengal, India
3Department of Physiology, Medical College and Hospital, Kolkata, W.B, India
4Department of Informatics and Mathematics, Mercer University, Macon, GA, USA
5Department of Statistics, University of Delhi, Delhi, India
6Department of Big data and Applied Statistics, Dongguk University, Gyeongju, Korea
7Department of Statistics, The University of Burdwan, Burdwan, West Bengal, India
Rabindra Nath Das, Department of Statistics, The University of Burdwan, Burdwan, West Bengal, India, Email: rabin.bwn@gmail.com
Received: 16-Feb-2023, Manuscript No. OAR-23-89458; Accepted: 10-Mar-2023, Pre QC No. OAR-23-89458 (PQ); Editor assigned: 18-Feb-2023, Pre QC No. OAR-23-89458 (PQ); Reviewed: 28-Feb-2023, QC No. OAR-23-89458 (Q); Revised: 07-Mar-2023, Manuscript No. OAR-23-89458 (R); Published: 14-Mar-2023
Abstract
Many authors have reported that Prostate Cancer (PC) and Cardiovascular Disease (CVD) are strongly associated, while it is not yet well established. The current report examines this fundamental query by examining the associations of a PC biomarker known as serum Prostatic Acid Phosphatase (PAP) with CVD risk factors such as Diastolic Blood Pressure (DBP), Systolic Blood Pressure (SBP), along with CVD history, and classified CVD patients based on Electrocardiogram (EKG) status, and conversely. It is derived herein that PAP has no association with SBP and DBP, while the mean PAP level is significantly higher for non-CVD subjects (P=0.0179), than for CVD patients. The variance of PAP level is significantly more scattered for CVD patients (P=0.0190) than normal, and also it is significantly more scattered for normal subjects based on EKG (P=0.0249), than the others. On the other hand, the mean and variance of DBP have no relation with PAP. Only the variance of DBP is significantly more scattered for normal subjects (P=0.0004) than PC patients, and it is significantly more scattered for PC patients with bone metastases (BM) (P=0.0021) than normal. Again, mean SBP decreases (P=0.0621) if PAP rises, while it increases as the primary tumor size (P=0.0054) increases. A similar association is observed for the variance of SBP with PAP, that is SBP variance is negatively associated with PAP (P=0.0045). It can be concluded that the association between PC and CVD exists, which should be considered for the medical treatment process.
icsatc neodeme advancedstructurescorp floormachinebrush scpe jcamasonry sages-tunisie sbsteel technomailleplus bolkan vaalea nsblueprinting mycleanairdoctors nycgeneralproroofing gabgadgets prsnekkern uniquescaffoldingsystems villaguicciardini acerpackaging acjstucco prontointervento-multiservice printersupplygiant sarel takkatiimi dragonshollow mazelsupply alfalchetto reliablegeneralagency lckenterprises realizzazione-giardini dmcindustries shop chathambrass ilfaroservizi soilmechanicsdrilling colorfullyyours agcsound carriere carnavaldetournai falconauto codingxcamp davinci-trondheim thebestofcolumbia cooperativetissage outsourcedmarketingpros tlc dawnnhough doubleclick pdirealty hattrennet az-bizsolutions jamaistropdart frontdata unitycreations fortisarezzo bspo-ken codar-confection theboulders bakerpersonnel fantasyphotographyandvideo fuleky tanssikoulutria ladybi swimanddance scuolavelatoscana x-pack creativeglazing lucagnizio sigaretteelettronichepisa mayiindustries frigo-clim elgars leoemma hotelalcantara el-pro therefore thebestofjacksonville nykran masmoudi thebestofspokane cogepre detrecruitment laresidencelepartage chimneycompanyboston awarepedia res-botanica recipefy semap thebestofcincinnati bb-one fourtech thebestofjoliet ajproduce jerryshulmanproduceshipper lckcabinetryny drivingtechniquesmadeeasy accademiaestetica pizzamaison schoonheidssalonbianca cabinsbrevardnc mrbrushes atlasrolloff hatip-medikal vezcocorporation thebestofcoloradosprings filtaclean monteleeper flyfisher ellatafa associazionepugliesiapisa unitycreationsltd maketeamstudiot douglasclear packagingpro softm allstarbeerinc burtonsupply footballscouting profondacreation johnvravickddsms fireislandbuilder advancedcontrolsolutions chittorgarhtaxiservices live-now orologeriatoscana racinemode thebestofwilmington agro-services violiner sandinghouse the-complete-package thebestofrichmond rcollision meubleskarray mes-recettes lawsandtaxes tavgrupp mkproducts royscottmarine taxi contreras-stockman sigmaweb de-noord thebestofkansascity maisonmedicaledelaeken recycledrubberpavers surfacingsystems unitedfidelityinc enokplan hunterremodeling edmersupply amerequipint sanilabcorp igglesis christiannursingregistry united-royal cantodelfiume northsidedeliny menuiserie-delbart passeritartufi justmyvoice ablefiresprinklers accantoalcentro ckperformance khalfallahpneus anti-flood-barriers bmstyle autosangiorgio-mercedes-benz carmagnino viipurinurheilijat multipack cma-eng mcafeerealty adrianaperciballi loconteedilecostruzioni konarprecision unityrubberco unityrubberproducts dante tela marathongranite baltimahalworcester heimdalbygg alstateprocessservice italydreamtour wemcocastingllc yachtbritesigns ecoledecroly-renaix anchorseniorapartments royalburton sk-veilag giannacapoti hubiteg customcommercialconstruction edm-nivelles probat-tunisie bachlawyer robertex inbora gpbconstruction tekstschrijver-tim bdsit trepro himalayanlounge lazersharpplumbing nycollisionking marinanova gealcorp nygabe maritimecoverage justmyvoice jukumech quimicolsa hayat-med aldrovandiauto michaelbenaltinc korenas sandvet americanmufflerautorepair justmyvoice liacoustics dminteriors agenziapromotech ligbtour internormfirenze justmyvoice zouila kohalmiferenc ashgroveresort ilmacinapepe suzukibandit hihna islandfishli prontointerventofabbro24h thebestofmidland thebestofportland dsgnaturaeambiente rimpex-medical giadaguidi royalroseappliances normas monicavignoliniluxury reddalsand defigners projektorilamput qtbservices labandas totalconceptdesign elannonnayttamo begmaterialiedili bardsdans samuelmanndds marksmenmfg demo17 chinafinewines coralia ivar-moe tournailesbains consew luisaprofumeriashop chimneycompanywestchester danapoly 268dental uspaerospace melonerp matcoservice emperorsoft cantare fninc greenpowerchemical westendsupply domobios unitysurfacingsystems martemoen hamptonssepticservices housatonicpaper sj-transport epsl-tunisie sungoldabrasives collinscreative barbarottomachinery soep thebestofalexandria straightlineconst itcimpianti hattrem-trafikkskole federalnetworks ppattorneys ceteau fbperformance coltgateway coolservice4u garaconfection bellformalwear abcconcretepumping mysantaria accurateindustrialmachining schmugerhardware thebestofjackson bellwetherstaffing sweetkarmadesserts tonerhuset mongilschool polycliniquelaouani buonidentro schoolbusmirrorsonline qlstransportation andereuropa cleanpressiondrycleaner bsyd planetlimony thebestoflasvegas csgmfoodequip potensial potiez invitiing tomscorvetteshop thebestbaltimorebusinesses honefoss thebestofoakland hydeparkdenim scmanndds sirreal totalpreferredsupply futureshockcorp myrtun
Keywords
bone metastases, cardiovascular disease, prostate cancer, serum prostatic acid phosphatase, serum prostatic acid phosphatase
Introduction
Prostate Cancer (PC) is one of the most powerful cancers in men. In the European and American male populations, PCassociated death is ranked second among all cancer-connected deaths, yet its etiology was not marked out [1-3]. However, PC may be completely cured if it is detected in its early stage, while other cancers are very difficult to treat. For early detection of PC, some biomarkers such as Prostate-Specific Antigen (PSA), serum Prostate Acid Phosphatase (PAP), Prostate Specific Membrane Antigen (PSMA), and Prostate Stem Cell Antigen (PSCA) are commonly used [4-8]. It was first noticed by Gutman and Gutman in 1938 that the PAP’s functional activity was increased in the circulation of PC patients [9]. Later on, it was proved that PAP was highly connected with PC progression, which was supported by many authors such as Small et al. and Sheridan et al. [10, 11].
It is commonly observed that the PC treatment’s late effect is CVD, and the supporting biological mechanisms consider a strong hormone manipulation cardio-toxic effect, or an indirect CVD effect through metabolic mechanisms [12-19]. PC literature review shows inconsistent relationships between PC and CVD risk factors in different ages, PC stages, follow-up time lengths, therapy types, and CVD outcomes [20, 21]. Some articles have studied CVD risk outcomes for PC patients along with non-PC patients, which have shown different findings [20, 21]. Therefore, the present literature shows an inconsistent relationship between PC and CVD.
The relationship between PC and CVD is still controversial. Several authors attempted to focus on it based on percentage, ratio, or simple correlation, which are not statistically significant [1,12-20,22]. In addition, previous authors conclude the existence of the above relationship through confounders, without proper modelling of the response with the explanatory factors [1, 22-24]. For instance, the article concluded that two-thirds of men with PC are at high CVD risk [1]. There is a direct connection between a plan to use Androgen Deprivation Therapy (ADT) and baseline CVD risk factors. However, this direct connection is expressed by confounding factors without proper statistical modelling [1,12,15,22-24]. Therefore, all the previous studies invite many doubts and debates.
The relationship between CVD and PC may be focused on in the following ways. Every PC biomarker (or risk factor) is to be modelled on all the remaining factors along with the CVD risk factors. Conversely, every CVD risk factor is to be modelled on all the remaining factors along with PC biomarkers. From all possible probabilistic models, it may be concluded about the association between CVD and PC. In the present study, the considered data set contains some PC factors such as serum Prostatic Acid Phosphatase (PAP) (a PC biomarker), study unit’s stage (0=no cancer; 1=prostate cancer); primary tumor size; tumor index stage and histolic grade; bone metastases (0=no, 1=yes). On the other hand, the considered data set contains some CVD factors such as SBP, DBP, the subject’s CVD history (0=no, 1=yes), the subject’s CVD stage identified by electrocardiogram code (0=normal; 1=benign; 2=heart strain; or rhythmic disturb & electrolyte; or conduction; or heart block; old Myocardial Infarction (MI); or recent MI). The current report examines the following hypothesis.
1. Is there any association between PAP with CVD factors? If it is affirmative, what are the resultant associations?
2. Is there any association between DBP with PC factors? If it is affirmative, what are the resultant associations?
3. Is there any association between SBP with PC factors? If it is affirmative, what are the resultant associations?
The article inquires about the above three relationship hypotheses connected to PC and CVD literature adopting the following sections such as materials & methods, statistical analysis, results & discussions, and conclusions. The three probabilistic models are displayed in Table 1 through 3 using the data set described in the materials section. These models are derived from Joint Generalized Linear Models (JGLMs), which are described in the methods section. The necessary derived results are focused on in the results and discussion section. Based on these three probabilistic models, the present article aims to reach conclusions.
Tab. 1. Results for PAP fitting of mean and dispersion models under Log-normal distribution
| Model | Covariate | JGLMs Log-normal fitted | |||
|---|---|---|---|---|---|
| estimate | Standard error | t(464) | P- value | ||
| Mean | Constant | -2.0336 | 0.439 | -4.632 | <0.0001 |
| Study unit’s stage (=SU-stage=E1)2 | 1.8521 | 0.1094 | 16.924 | <0.0001 | |
| Performance rating (=PER=E7)2 | 4.6645 | 2.4894 | 1.874 | 0.0616 | |
| Performance rating (=PER=E7)3 | 0.1095 | 0.1147 | 0.955 | 0.3401 | |
| Cardiovascular disease (=CVD=E8)2 | -0.1319 | 0.0555 | -2.376 | 0.0179 | |
| Bone metastases (=BM=E16)2 | 1.019 | 0.2425 | 4.203 | <0.0001 | |
| Estrogen (=RX=v3) | 0.0211 | 0.0145 | 1.449 | 0.148 | |
| Serum haemoglobin (=HG=v12) | 0.0378 | 0.0154 | 2.459 | 0.0143 | |
| Primary tumor size (SZ=v13) | 0.0087 | 0.0031 | 2.796 | 0.0055 | |
| Study date (S-date=v17) | 0.0003 | 0.0001 | 1.974 | 0.049 | |
| Dispersion | Constant | -0.3993 | 1.1926 | -0.335 | 0.7378 |
| Study unit’s stage (=SU-stage=E1)2 | 1.4617 | 0.194 | 7.534 | <0.0001 | |
| Cardiovascular disease (=CVD=E8)2 | 0.3395 | 0.1443 | 2.353 | 0.019 | |
| Bone metastases (=BM=E16) 2 | 0.7738 | 0.2226 | 3.476 | 0.0006 | |
| Estrogen (=RX=v3) | 0.0733 | 0.0348 | 2.103 | 0.036 | |
| Electrocardiogram (=EKG=E11)2 | -0.788 | 0.35 | -2.251 | 0.0249 | |
| Electrocardiogram (=EKG=E11)3 | -0.1309 | 0.1529 | -0.856 | 0.3924 | |
| Serum haemoglobin (=HG=v12) | -0.0799 | 0.0425 | -1.881 | 0.0606 | |
| Primary tumor size (SZ=v13) | 0.0129 | 0.0061 | 2.11 | 0.0354 | |
| Tumor index stage and histolic grade (=SG=v14) | 0.1286 | 0.0471 | 2.728 | 0.0066 | |
| Study date (S-date=v17) | -0.0005 | 0.0003 | -1.458 | 0.1455 | |
Materials and Methods
The relationship between CVD and PC is studied herein adopting a randomized clinical experimental data set that was executed on 474 men with 3rd or 4th PC stages. The data set was collected by D.P. Byar, who produced two articles based on this data set with his co-workers [25, 26]. The above data set was republished in the book by Andrews and Herzberg [27]. Regarding each experimental subject, the following characters/factors were investigated:
1. Study unit’s stage (SU-stage=E1) (0=no cancer; 1=prostate cancer)
2. Follow up months (=F-time=v2)
3. Estrogen (mg) (=RX=v3)
4. Survival status (Alive=E4) (0=Alive; 1=Dead due to PC; 2=Dead due to cerebrovascular; or vascular or heart; or pulmonary embolism; or other cancer; or other specific non-cancer; or respiratory disease; or unknown cause; or unspecified non-cancer)
5. Weight (=Wt=v5)
6. Age(=v6)
7. Performance rating (=PER=E7) (0=normal mobility; 1=confined to bed; 2=in bed<50% daytime; or in bed>50% daytime)
8. Cardiovascular disease (CVD=E8) history (0=no, 1=yes)
9. SBP=v9
10. DBP=x10
11. EKG=E11 code (0=normal; 1=benign; 2=heart strain; or rhythmic disturb & electrolyte; or conduction; or heart block; old myocardial infarction (MI); or recent MI)
12. Serum haemoglobin (=HG=v12)
13. Primary tumor size (SZ=v13)
14. Tumour index stage and histolic grade (=SG=v14)
15. Serum prostatic acid phosphatase (=PAP=v15)
16. Bone metastases (=BM=E16) (0=no, 1=yes);
17. Study date (S-date=v17).
The undertaken PC data set comprises seven attributes and ten continuous factors. In the present investigations, PAP, DBP, or SBP is taken as the continuous response variable, and the remaining others are treated as the explanatory variables/factors.
Statistical methods
In the current study, three considered responses such as PAP, DBP, and SBP are identified as heteroscedastic, which may be suitably modelled by stabilizing variance, but it may not be always stabilized [28]. For deriving better models, Joint Generalized Linear Models (JGLMs) under gamma, or lognormal distribution are adopted herein [29, 30]. The above method under both the distribution is illustrated in the books by Lee et al., and Das [29,31]. Recently, two articles by Das et al. used JGLMs along with R-codes in History for studying silver and gold production trends [32, 33]. JGLMs under both distributions are discussed very shortly for ready reference as follows.
JGLMs under log-normal distributed:
For the positive response Yi (=PAP, or DBP, or SBP) with E (Yi =PAP, or DBP, or SBP)=µi (mean) and Var(Yi =PAP, or DBP, or SBP)=σi2µi2=σi2 ( Vµi)say, where σi2's are dispersion parameters and V (.) reveals the variance function, generally the log transformation Zi =log (Yi =PAP, or DBP, or SBP) is applied to stabilize the variance Var(Zi)≈σi2,but the variance may not be stabilized always [28]. For developing an improved model, JGLMs for the mean and dispersion are considered. For the response PAP or DBP, or SBP assuming log-normal distribution, JGL mean and dispersion models (with Zi =log (Yi =PAP, or DBP, or SBP) are as follows:
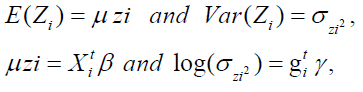
where X ti and g ti are the dependent or explanatory factors/variables vectors linked to the regression coefficients β and γ , respectively.
Gamma distributed JGLMs:
For the above-stated Yi ’s (=PAP, or DBP, or SBP), the variance has two components such as V(µi) (based on the mean parameters) and i σ (free of µi’s). The variance function V (.) reveals the GLM family distributions. For example, if V(µ)=µ, it is Poisson, gamma if V(µ) =µ2, and normal if V(µ)=1, etc. Gamma JGLMs mean and dispersion models are as follows:
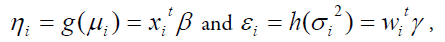
Where g(.) and h(.)are the GLM link functions associated with the mean and dispersion linear predictors respectively, and w ti , w ti, are the explanatory factors/variables vectors attached with the mean and dispersion parameters respectively. The Maximum Likelihood (ML) method is used for estimating mean parameters, while the Restricted ML (REML) method is applied for estimating dispersion parameters, which are explicitly stated in the book by Lee et al., [29].
Statistical & graphical analysis
Analysis of PAP:
The response PAP is modelled on the rest explanatory factors/ variables (described in the materials section) using JGLMs under both distributions. The final selected fitted model for PAP is accepted based on the lowest Akaike Information Criterion (AIC) value that minimizes both the squared error loss and predicted additive errors [34]. According to the AIC rule, the lognormal model fit (AIC=1399) of SPAP is better than the gamma fit (AIC=1590.239). The best log-normal fitted PAP analysis outcomes are shown in Table 1. In both the mean and dispersion models, the included factors are most significant and important for the models [34].
The data-derived PAP models are verified using graphical diagnostic tools. The final accepted fitted log-normal PAP joint models are examined in Figure 1. Figure 1(a) presents the absolute PAP log-normal JGL fitted absolute residuals plot concerning its predicted values, which is exactly a flat straight line, implying that variance is constant with the running means. Figure 1(b) reveals the PAP log-normal fitted mean model (normal probability plot, which does not reflect any fitting discrepancy. So, both Figures 1(a) & 1(b) imply that the PAP log-normal fitted JGLMs are close to the unknown PAP models.
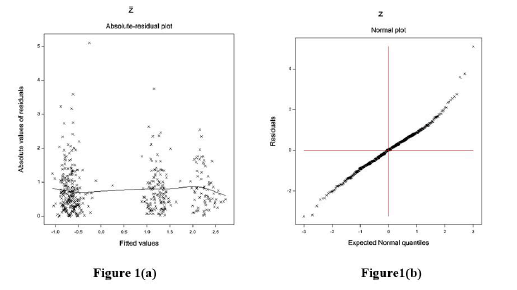
Figure 1: For the JGL log-normal PAP fit (Table 1), the (a) absolute residuals plot against the PAP fitted values, and (b) the normal probability plot for the PAP mean model.
Analysis of DBP
The response DBP is modeled on the rest explanatory factors/ variables (described in the materials section) using JGLMs under both distributions. The final selected fitted model for DBP is accepted based on the lowest AIC value [34]. According to the AIC rule, the gamma model fit (AIC=1433.133) of DBP is better than the log-normal fit (AIC=1448). The best gamma-fitted DBP analysis outcomes are shown in Table 2. In both the mean and dispersion models, the included factors are all statistically significant.
Tab. 2. Results for DBP fitting of mean and dispersion models under Gamma distribution
| Model | Covariates | estimate | Standard error. | t(470) | P-value |
|---|---|---|---|---|---|
| Mean | Constant | 1.5564 | 0.08487 | 18.34 | <0.0001 |
| Serum haemoglobin (=HG=v12) | 0.008 | 0.00333 | 2.39 | 0.0172 | |
| Age (=v6) | -0.0031 | 0.00087 | -3.61 | 0.0003 | |
| SBP(=v9) | 0.0457 | 0.00265 | 17.27 | <0.0001 | |
| Dispersion | Constant | -4.192 | 0.1347 | -31.13 | <0.0001 |
| Study unit’s stage (=SU-stage=E1)2 | -0.452 | 0.1562 | -2.892 | 0.0004 | |
| Cardiovascular disease(=CVD=E8)2 | 0.256 | 0.1389 | 1.844 | 0.0602 | |
| Bone metastases (=BM=E16) 2 | 0.64 | 0.207 | 3.091 | 0.0021 | |
| Electrocardiogram (=EKG=E11)2 | 0.336 | 0.3279 | 1.026 | 0.3054 | |
| Electrocardiogram (=EKG=E11)3 | 0.286 | 0.1426 | 2.003 | 0.0457 |
The data obtained from DBP models are examined by applying graphical diagnostic tools. The final selected gamma JGL fitted DBP models are examined in Figure 2. Figure 2(a) presents the absolute DBP gamma JGL fitted residuals plot concerning its predicted values that is nearly a flat straight line, indicating that variance is equal with the running means. Figure 2(b) presents the JGL gamma fitted DBP mean model normal probability plot that does not reveal any lack of fitting. Therefore, both these Figures 2(a) and 2(b) indicate that the JGL gamma-fitted DBP models are similar to the true DBP models.
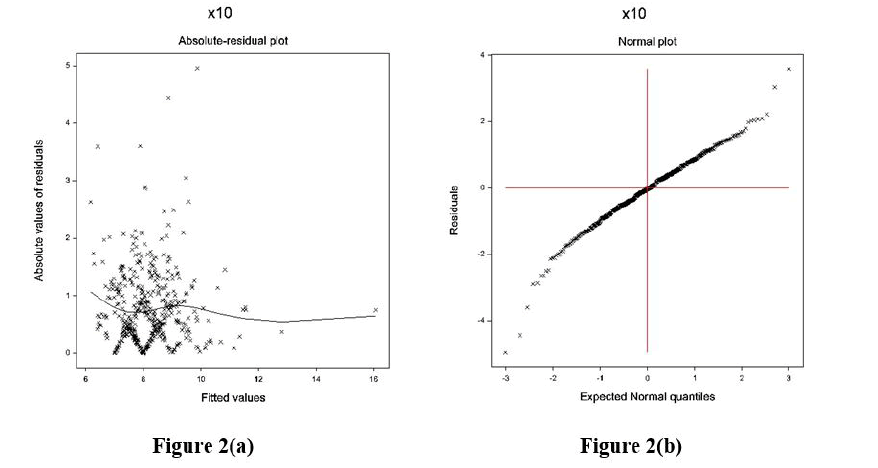
Figure 2: For the JGL gamma DBP fit (Table 2), a. absolute residuals plot against the DBP fitted values, and b. the normal probability plot for the DBP mean model.
Analysis of SBP
The response SBP is modelled on the rest explanatory factors/ variables (described in the materials section) using JGLMs under both distributions. The final selected fitted model for SBP is accepted based on the lowest AIC value [34]. According to the AIC rule, the log-normal model fit (AIC=1862) of SBP is better than the gamma fit (AIC=1864.812). The best log-normal fitted SBP analysis outcomes are shown in Table 3. In both the mean and dispersion models, the included factors are all statistically significant.
Tab. 3. Results for SBP fitting of mean and dispersion models under Log-normal distribution
| Model | Covariates | JGLMsÃÂ? ÃÂ? Log-normal fit | |||
|---|---|---|---|---|---|
| estimate | Standard error. | t(468) | P-Value | ||
| Mean | constant | 1.8191 | 0.06405 | 28.402 | <0.0001 |
| Age (=v6) | 0.0032 | 0.00075 | 4.196 | <0.0001 | |
| Cardiovascular disease(=CVD=E8)2 | 0.0202 | 0.01177 | 1.718 | 0.0864 | |
| DBP(=x10) | 0.0708 | 0.00367 | 19.296 | <0.0001 | |
| Primary tumor size (SZ=v13) | 0.0013 | 0.00046 | 2.796 | 0.0054 | |
| Prostatic acid phosphatase (=PAP=v15) | 0.0001 | 0.00002 | -1.87 | 0.0621 | |
| Dispersion | Constant | -2.2205 | 0.5583 | -3.977 | <0.0001 |
| Cardiovascular disease(=CVD=E8)2 | 0.3273 | 0.1375 | 2.38 | 0.0177 | |
| DBP(=x10) | -0.0822 | 0.0363 | -2.264 | 0.0085 | |
| Electrocardiogram (=EKG=E11)2 | 0.375 | 0.3254 | 1.152 | 0.2499 | |
| Electrocardiogram (=EKG=E11)3 | 0.3503 | 0.1464 | 2.394 | 0.0171 | |
| Serum haemoglobin (=HG=v12) | -0.1207 | 0.0377 | -3.203 | 0.0015 | |
| Prostatic acid phosphatase (=PAP=v15) | -0.0045 | 0.0016 | -2.858 | 0.0045 | |
The data executed by SBP models are verified by graphical diagnostic tools. The final considered SBP-fitted JGL log-normal mean and dispersion models are tested in Figure 3. Figure 3(a) represents the absolute SBP log-normal JGL fitted residuals plot against its predicted values that is almost a flat straight line, except for the two tails, indicating that variance is equal with the running means. The left tail is increasing as a larger absolute residual is located at the left boundary, while the right tail is decreasing as a smaller absolute residual is located at the right boundary. Figure 3(b) represents the SBP log-normal fitted mean model normal probability plot, which shows no fit discrepancy. So, these two figures imply that the SBP log-normal fitted JGLMs is similar to the unknown true SBP models.
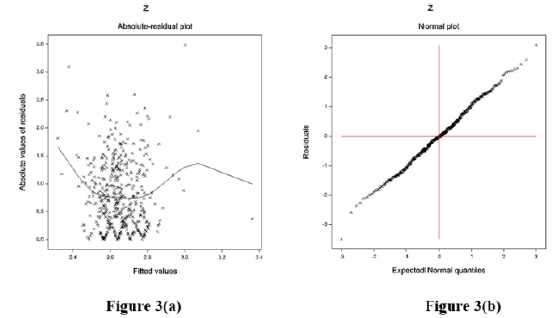
Figure 3: For the JGL log-normal SBP fit (Table 1), a. absolute residuals plot against the SBP f itted values, and b. the normal probability plot for the SBP mean model.
Results and Discussion
According to the present study's aims, two sets of variables/factors are considered from all 17 factors/variables from the considered PC data set (in the material section). One set of covariates is PCrelated factors/variables, which is termed as PC-set and the other set of covariates is CVD-related factors/variables, which is termed as CVD-set. Note that the PC-set contains 6 elements (variables/ factors}, which is denoted by PC-set ={Study unit’s stage (SUstage=E1) (0=no cancer, 1=prostate cancer), performance rating (=PER=E7) (0=normal mobility; 1=confined to bed; 2=in bed<50% daytime; or in bed>50% daytime), primary tumour size (SZ=v13), tumor index stage and historic grade (=SG=v14), serum prostatic acid phosphatase (=PAP=v15); bone metastases (=BM=E16) (0=no, 1=yes)}, while the CVD set contains 5 elements (variables/ factors), which is denoted by CVD-set ={Cardiovascular disease (CVD=E8) history (0=no, 1=yes), SBP=v9, DBP=x10, EKG=E11 code (0=normal; 1=benign; 2=heart strain; or rhythmic disturb & electrolyte; or conduction; or heart block; old Myocardial Infarction (MI); or recent MI)}. T he present article examines the relationship of a factor/variable of PC-set with any other factor/variable of CVD-set, and conversely. T he analyses of PAP from the PC set, DBP, and SBP from the CVD set have been derived above in the current report. Based on these analyses, the relationships between PC and CVD are examined herein. Therefore, only the related results are mentioned herein, even though there are many results in the three analyses.
Results of pap
From Table 1 (PAP analysis), it is derived herein that the mean and variance of PAP have no association with SBP and DBP, while the mean PAP level is significantly negatively associated with CVD history (P=0.0179). The variance of PAP level is significantly positively associated with CVD history (P=0.0190), while it is significantly negatively associated with the second level of EKG (P=0.0249).
JGL log-normal fitted PAP level mean model Table 1 is Estimated log(PAP)=--2.0336+1.8521 SU-stage2+4.6645 PER2+0.1095 PER3-0.1319 CVD2+1.0190 BM2+0.0211 RX +0.0378 HG +0.0087 SZ +0.0003S-date, and the JGL og-normal fitted PAP variance x (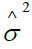 )model from Table 1 is
)model from Table 1 is 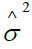 =exp (--0.3993+1.4617 SU-stage2 +0.3395 CVD2 +0.7738 BM2 +0.0733 RX--0.7889 EKG2--- 0.1309 EKG3--0.0799 HG+0.0129 SZ+0.1286 SG --0.0005 S-date).
=exp (--0.3993+1.4617 SU-stage2 +0.3395 CVD2 +0.7738 BM2 +0.0733 RX--0.7889 EKG2--- 0.1309 EKG3--0.0799 HG+0.0129 SZ+0.1286 SG --0.0005 S-date).
From Table 1 (PAP analysis), the mean PAP level is not directly associated with SBP and DBP.
Results Of Dbp
From Table 2 (DBP analysis), it is obtained that the mean and variance of DBP have no relation with PAP. Only the variance of DBP is significantly negatively associated with the study unit’s stage (SU-stage) (P=0.0004), and it is significantly positively associated with bone metastases (BM) (P=0.0021).
GL gamma fitted DBP level mean model Table 2 is 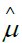 =exp (1.5564+0.0080 HG--0.0031 Age+0.0457 SBP), and the JGL gamma fitted DBP level variance
=exp (1.5564+0.0080 HG--0.0031 Age+0.0457 SBP), and the JGL gamma fitted DBP level variance 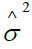 model from Table 2 is
model from Table 2 is 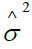 =exp(--4.192--0.452 SU-stage2 +0.256 CVD2 +0.640 BM2 +0.336 EKG2 +0.286 EKG3 ).
=exp(--4.192--0.452 SU-stage2 +0.256 CVD2 +0.640 BM2 +0.336 EKG2 +0.286 EKG3 ).
Results Of SBP
From Table 3 (SBP analysis), it is developed that mean SBP is partially negatively associated with Prostatic Acid Phosphatase (PAP) (P=0.0621), while it is significantly positively associated with the primary tumor size (SZ) (P=0.0054). The variance of SBP is significantly negatively associated with PAP (P=0.0045).
JGL log-normal fitted SBP level mean model Table 3 is Estimated log(SBP)=1.8191+0.0032 Age +0.0202 CVD2 +0.0708 DBP+0.0013SZ-0.0001 PAP, and the JGL log-normal fitted
SBP level dispersion 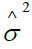 model from Table 3 is
model from Table 3 is 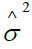 =exp (-2.2205+0.3273 CVD2--0.0822 DBP+0.3750 EKG2 +0.3503 EKG3--0.1207 HG--0.045 PAP).
=exp (-2.2205+0.3273 CVD2--0.0822 DBP+0.3750 EKG2 +0.3503 EKG3--0.1207 HG--0.045 PAP).
Discussions
PAP analysis outcomes and models are displayed above. From Table 1, it is obtained that there is no association between PAP and hypertension risk factors such as SBP and DBP both in the mean and dispersion models. It is derived herein that the mean PAP level is significantly negatively associated with CVD history (P=0.0179) (0=no, 1=yes), implying that PAP level is higher for non-CVD patients than CVD patients, who were under PC with third and fourth stage. It shows that mean PAP level is a protective factor for CVD, and it has no direct (or positive) association with CVD. The variance of PAP level is significantly positively related to CVD history (P=0.0190) (0=no, 1=yes), implying that PAP level is more dispersed for CVD patients than non-CVD. Also, the variance of PAP level is inversely related to the second level of EKG (P= 0.0249), and it is insignificant at the third level (P=0.3924) (0=normal; 1=benign; 2=heart strain; or rhythmic disturb & electrolyte; or conduction; or heart block; old Myocardial Infarction (MI); or recent MI), interpreting that PAP level is more dispersed for the normal subjects without heartdisease related problems that were identified by EKG than the others with heart-disease related problems.
DBP analysis outcomes and models are displayed above. From Table 2, it is derived that the mean and variance of DBP level have no relation with PAP level. It is derived herein that the variance of DBP is significantly inversely related to the study unit’s stage (SUstage) (P=0.0004) (0=no cancer; 1=prostate cancer), indicating that DBP level is more dispersed for normal subjects than PC patients. Also, the variance of DBP is significantly directly related to Bone Metastases (BM) (P=0.0021) (0=no, 1=yes), concluding that DBP level is more dispersed for PC subjects with BM than others.
SBP analysis outcomes Table 3, and models are displayed above. From Table 3, it is derived that mean SBP is partially inversely related to PAP (P=0.0621), implying that the SBP level is lower for the subjects with higher PAP levels. It shows that PAP is a protective factor against SBP. Also, the mean SBP level is significantly directly related to the primary tumor size (P=0.0054), interpreting that the SBP level increases as the primary tumor size increases. From Table 3, it is observed that PAP level is directly related to primary tumor size (P=0.0054), so the PC subjects with bigger primary tumors should have higher PAP levels, therefore, they may have lower SBP levels. So, PC subjects with bigger primary tumors may not have higher SBP levels. Therefore, PC subjects without a CVD history may have normal SBP levels. Even though there is a direct association between SBP and PC subjects’ primary tumor size, it does not affect SBP as there is an inverse association between SBP and PAP. The variance of SBP is significantly inversely related to PAP (P=0.0045), implying that the SBP level is more dispersed for the subjects with lower PAP levels.
From the above three models (PAP, DBP, and SBP), it has been derived that there are some associations between the two sets such as PC-set and CVD-set. So, one can conclude that there are some associations between CVD and PC diseases. It has been observed herein that even though there are some associations between PC and CVD, they may not be identified by percentages, as PAP acts as a protective factor for CVD. Again, there are some complicated associations between SBP and PC-set, as shown above in the SBP analysis. Due to these complicated relationships, it is shown herein that PC subjects are not affected highly by CVD risk factors. T herefore, earlier research could not identify the associations between PC disease and CVD.
The present findings between the associations of PC-set and CVD-set have been derived herein using JGLMs as the considered responses are heteroscedastic. All the previous articles tried to establish these relationships using simple correlation and regression, percentages, and meta-analysis which are not suitable for heteroscedastic data sets. The article has shown several associations between PC-set and CVD-set using mean and dispersion models, which are very little focused on in the previous articles. One can examine the present associations between the PC set and CVD set using the data mentioned in the materials section. In the current report, only the PC biomarker PAP is considered, while other biomarkers such as PSA, PSMA, and PSCA can be considered. The other biomarkers are not considered herein as the considered data set does not contain information on these biomarkers. Similarly, one can consider other CVD risk factors such as heart rate, basal blood pressure, ejection fraction, etc.
Conclusion
The relationships between PC-set and CVD-set are identified herein using probabilistic modelling. The accepted models are taken based on the lowest AIC, graphical examinations, comparison of two distributions, and the small standard error of the estimates. The above associations are derived herein based on the selected final models, where models are verified by graphical examinations. Best of our knowledge, these above associations are not reported in any previous articles. The other PC biomarkers and CVD risk factors will be considered in our subsequent studies. T he current research has established the association between PC disease and CVD. It may remove the controversial ideas between PC disease and CVD. It may help the researchers and practitioners. It can be concluded that the association between PC and CVD exists, which should be considered for the medical treatment process. Care should be taken for PC disease and CVD in older ages of men.
Funding Resources
The work of Shipra Banik was supported by the Independent University, Bangladesh (IUB) Faculty Research Fund.
Acknowledgement
The authors are very grateful to the principal data investigator D.P. Byar (National Cancer Institute), who provided the data freely for scientific study.
Conflicts of Interest
The authors confirm that this article's content has no conflict of interest.
References
- Leong DP, Fradet V, Shayegan B, Duceppe E, Siemens R, et al. Cardiovascular risk in men with prostate cancer: insights from the radical pc study. J. Urol. 2020; 203:1109-1116.
- Hsing AW, Chokkalingam AP. Prostate cancer epidemiology. Front. Biosci. -Landmark. 2006; 11:1388-1413.
- Kong HY, Byun J. Emerging roles of human prostatic acid phosphatase. Biomol. ther. 2013;21:10.
- Hobisch A, Eder IE, Putz T, Horninger W, Bartsch G, et al. Interleukin-6 regulates prostate-specific protein expression in prostate carcinoma cells by activation of the androgen receptor. Cancer res. 1998;58:4640-4645.
[Google Scholar] [Crossref]
- Bussemakers MJ, Van Bokhoven A, Verhaegh GW, Smit FP, Karthaus HF, et al. Dd3: A new prostate-specific gene, highly overexpressed in prostate cancer. Cancer res. 1999; 59:5975-5979.
[Google Scholar] [Crossref]
- Gupta A, Lotan Y, Ashfaq R, Roehrborn CG, Raj GV, et al. Predictive value of the differential expression of the urokinase plasminogen activation axis in radical prostatectomy patients. Eur. Urol. 2009; 55:1124-1134.
- Madu CO, Lu Y. Novel diagnostic biomarkers for prostate cancer. J. Cancer. 2010; 1:150.
- Batta A, Panag KM, Singh J. Diagnosis of prostate cancer---Role of biomarkers. Int. J. Cur. Biomed. Phar. Res. 2012; 2:339-345.
[Google Scholar] [Crossref]
- Gutman AB, Gutman EB. An “acid” phosphatase occurring in the serum of patients with metastasizing carcinoma of the prostate gland. J. Clin. investig. 1938; 17:473-478.
[Google Scholar] [Crossref]
- Small EJ, Schellhammer PF, Higano CS, Redfern CH, Nemunaitis JJ, et al. Placebo-controlled phase III trial of immunologic therapy with sipuleucel-T (APC8015) in patients with metastatic, asymptomatic hormone refractory prostate cancer. J Clin Oncol. 2006; 24:3089-3094.
- Sheridan T, Herawi M, Epstein JI, Illei PB. The role of P501S and PSA in the diagnosis of metastatic adenocarcinoma of the prostate. Am. j. Surg. Pathol. 2007; 31:1351-1355.
- Jonusas J, Drevinskaite M, Patasius A, Kincius M, Janulionis E, et al. Androgen-deprivation therapy and risk of death from cardiovascular disease in prostate cancer patients: a nationwide lithuanian population-based cohort study. Aging Male. 2022; 25:173-179.
- Wilk M, Wasko-Grabowska A, Szmit S. Cardiovascular complications of prostate cancer treatment. Front. Pharmacol. 2020; 11:555475.
- Davis MK, Rajala JL, Tyldesley S, Pickles T, Virani SA. The prevalence of cardiac risk factors in men with localized prostate cancer undergoing androgen deprivation therapy in British Columbia, Canada. J. Oncol. 2015.
- Moustsen IR, Larsen SB, Duun-Henriksen AK, Tjønneland A, Kjaer SK, et al. Risk of cardiovascular events in men treated for prostate cancer compared with prostate cancer-free men. Br. j. cancer. 2019; 120:1067-1074.
- Conteduca V, Di Lorenzo G, Tartarone A, Aieta M. The cardiovascular risk of gonadotropin releasing hormone agonists in men with prostate cancer: an unresolved controversy. Crit. rev. oncol./hematol. 2013; 86:42-51.
- De Haas EC, Oosting SF, Lefrandt JD, Wolffenbuttel BH, Sleijfer DT, et al. The metabolic syndrome in cancer survivors. Lancet oncol. 2010; 11:193-203.
- Lenihan DJ, Cardinale DM. Late cardiac effects of cancer treatment. J. Clin. Oncol. 2012; 30:3657-3664.
- Kintzel PE, Chase SL, Schultz LM, O'Rourke TJ. Increased risk of metabolic syndrome, diabetes mellitus, and cardiovascular disease in men receiving androgen deprivation therapy for prostate cancer. Pharmacother.: J. hum. Pharmacol. drug ther. 2008; 28:1511-1522.
- Armenian SH, Xu L, Ky B, Sun C, Farol LT, et al. Cardiovascular disease among survivors of adult-onset cancer: a community-based retrospective cohort study. J. Clin. Oncol. 2016; 34:1122.
- O'Farrell S, Garmo H, Holmberg L, Adolfsson J, Stattin P, et al. Risk and timing of cardiovascular disease after androgen-deprivation therapy in men with prostate cancer. J. Clin. Oncol.: off. j. am. soc. Clin. Oncol. 2015; 33:1243-1251.
- Liang Z, Xie B, Li J, Wang X, Wang S, et al. Hypertension and risk of prostate cancer: a systematic review and meta-analysis. Sci. rep. 2016; 6:1-7.
- Seretis A, Cividini S, Markozannes G, Tseretopoulou X, Lopez DS, et al. Association between blood pressure and risk of cancer development: a systematic review and meta-analysis of observational studies. Sci. rep. 2019;9:1-2.
- Wilk M, Wasko-Grabowska A, Szmit S. Cardiovascular complications of prostate cancer treatment. Front. Pharmacol. 2020; 11:555475.
- Byar DP, Corle DK. Selecting optimal treatment in clinical trials using covariate information. J. chronic dis. 1977; 30:445-59.
- Byar DP, Green SB. The choice of treatment for cancer patients is based on covariate information. Bull. du cancer. 1980; 67:477-490.
[Google Scholar] [Crossref]
- Andrews DF, Herzberg AM. Data: a collection of problems from many fields for the student and research worker. Springer sci. bus. Media. 2012.
[Google Scholar] [Crossref]
- Myers RH, Montgomery DC, Vining GG, Robinson TJ. Generalized linear models: with applications in engineering and the sciences. John Wiley sons. 2012.
[Google Scholar] [Crossref]
- Lee Y, Nelder JA, Pawitan Y. Generalized linear models with random effects: unified analysis via H-likelihood. Chapman hall/CRC; 2018.
- Das RN, Lee Y. Log-normal versus gamma models for analyzing data from quality-improvement experiments. Qual. eng. 2008; 21:79-87.
- Das RN. Robust response surfaces, regression, and positive data analyses. CRC Press. 2014.
[Google Scholar] [Crossref]
- Raykundaliya DP. Mahashweta Das, Malabika Ray, Anil Kumar Sarkar, Vasant Patel. History of new world silver production trends between 1521--1810. Journal of Econom. stat. 2021; 1:43-59.
[Google Scholar] [Crossref]
- Das M, Ray M, An H, Lee Y. The history of Portuguese and Spanish colonies gold yield’s trend from 1492-1810.
[Google Scholar] [Crossref]
- Hastie T, Tibshirani R, Friedman JH, Friedman JH. The elements of statistical learning: data mining, inference, and prediction. N. Y.: Springer. 2009. [Google Scholar] [Crossref]