Research Article - Onkologia i Radioterapia ( 2022) Volume 16, Issue 10
Role of Serum Prostatic Acid Phosphatase on Prostate Cancer Patients
Jinseog Kim1, Mahashweta Das2, Ishita Saha3, Gaurab Bhattacharyya4, Sabyasachi Mukherjee4, Ranjan Kumar Sahoo5, Rajyalakshmi Kottapalli6, Rajkumari Sanatombi Devi7, Sunit Kumar Medda8 and Rabindra Nath Das4*2Department of History, The University of Burdwan, Burdwan, West Bengal, India
3Department of Physiology, Medical College and Hospital, Kolkata, West Bengal, India
4Department of Statistics, The University of Burdwan, Burdwan, West Bengal, India
5School of Statistics, G. M. University, Sambalpur, Odisha, India
6Department of Computer Science and Engineering, Koneru Lakshmaiah Education Foundation, Greenfileds,, India
7Department of Statistics, Moreh College, Moreh, Manipur, India
8Kalyani J.N.M. Hospital, Kalyani, Nadia, West Bengal, India
Rabindra Nath Das, Department of Statistics, The University of Burdwan, Burdwan, West Bengal, India, Email: rabin.bwn@gmail.com
Received: 19-Sep-2022, Manuscript No. OAR-22-75061; Accepted: 10-Oct-2022, Pre QC No. OAR-22-75061 (PQ); Editor assigned: 21-Sep-2022, Pre QC No. OAR-22-75061 (PQ); Reviewed: 04-Oct-2022, QC No. OAR-22-75061 (Q); Revised: 09-Oct-2022, Manuscript No. OAR-22-75061 (R); Published: 13-Oct-2022
Abstract
It is well known that serum prostatic acid phosphatase (SPAP) may have a great role on Prostate Cancer Patients (PCPs), but its effects are not clearly identified in the prostate cancer literature. The current article aims to identify the effects of SPAP on PCPs. It is derived herein that mean SPAP level is higher for PCPs (P<0.0001) and PCPs confined to bed (P=0.0794) than normal. Mean SPAP level is higher for PCPs with Bone Metastases (BM) (P<0.0001), and it is lower for cardiovascular disease history patients (CDHPs) (P=0.0188) than normal. Mean SPAP level is positively connected with estrogen level (P=0.1148) in the log-normal fitted model, while it is highly significant (P<0.0001) in the gamma fitted model. In addition, mean SPAP level is positively related with Serum Hemoglobin (SHG) (P=0.0167), size of primary tumor (P=0.0092) and study time (P=0.0463). Variance of SPAP level is higher scattered for PCPs (P<0.0001), and PCPs with BM (P=0.0005), or CDHPs (P=0.0113) than normal. Again, variance of SPAP level is positively related with diastolic blood pressure (DBP) (P=0.0433), estrogen level (P=0.0225), size of primary tumor (SZ) (P=0.0915) and index of tumor stage and histolic grade (SG) (P=0.0155), while it is negatively connected with electrocardiogram status (P=0.0229) and SHG (P=0.0340). The report concludes that SPAP is highly associated with PCPs and along with their many factors such as SHG, estrogen level, BM, size of primary tumor, DBP etc.
Keywords
Bone Metastases (BM), Cardiovascular Disease History Patients (CDHPS), estrogen level, Prostate Cancer Patients (PCPS), Serum Prostatic Acid Phosphatase (SPAP), non-constant variance
Introduction
Prostate Cancer (PC) is one of the most dominant cancers in men. In the United States of America, PC related death is ranked second among all cancer related deaths in men, but it’s an etiology has not been clearly identified yet [1, 2]. However, in comparison to some other cancers, which are very difficult to treat, PC can be completely cured if it is identified in its early stage. There are many PC biomarkers such as Prostate Specific Membrane Antigen (PSMA), Prostate Stem Cell Antigen (PSCA), Prostate-Specific Antigen (PSA) and Serum Prostate Acid Phosphatase (SPAP) have been identified, which are helpful to detect earlier PC [3-8].
In 1938, Gutman and Gutman first discovered that the functional activity of SPAP was increased in the circulation of the PCPs [910,11]. Veeramani et al. established that SPAP was highly associated with PC progression in PCPs, and it could be considered as a biochemical indicator or biomarker for PC treatment [12]. Consequently, SPAP was widely examined as a PC representative biomarker until the foundation of ProstateSpecific Antigen (PSA) as the standard new biomarker [12, 13]. After the introduction of PSA examining in blood, it has been widely used for identifying PCPs. Kong and Byun discussed the different PC biomarkers [2].
It is believed that SPAP is the principal regulator of prostate cell growth, but its exact functional role in normal prostate as well as its detailed molecular mechanism regulation is still unclear [2, 7, 12-14]. A recent article by Balakrishna focuses on the effects of SPAP on liver biochemical parameters [15]. In addition, there is very little study of the role of SPAP on anatomical characters, biochemical parameters and cardiac factors etc. of the subjects [1,2,13,15, 16-18].
The article aims to examine the functional activities of SPAP on PCPs, which are equivalent to some hypothesis-testing prostate cancer research. In practice for establishing a causal relationship (i.e., cause-and-effect) among the explanatory variables/factors, the investigators need to establish an appropriate stochastic, or probabilistic model that can represent the relationships among the explanatory variables/factors. In the earlier PC studies, there are very little cause-and-effect studies [2,15,18]. Practically, the effect is considered as the dependent variable, while the causes are treated as the explanatory factors/variables. The article examines the following prostate cancer research queries.
1. What are the determinants of SPAP? This is the primary query in prostate cancer epidemiology.
2. How can one derive the determinants of SPAP?
3. What are the roles of SPAP on anatomical, biochemical, cardiac factors of the subjects?
The article focuses on these three above queries describing the sections materials & methods, statistical analysis, results & discussions, and conclusions. The derived determinants of SPAP are noted in Table 1, while the determinants are derived by Joint Generalized Linear Models ( JGLMs), and the effects of SPAP are focused in the discussion section.
Tab. 1. Results for SPAP fitting of mean and dispersion models under Log-normal and Gamma
| Model | LOG-NORMAL MODEL FIT | GAMMA MODEL FIT | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Covariate | Estimate | s.e. | t(463) | P-Value | Estimate | s.e. | t(463) | P-Value | |
| Mean | Constant | -2.0284 | 0.4407 | -4.603 | <0.0001 | -1.782 | 0.5091 | -3.5 | 0.0005 |
| Stage (V1)2 | 1.8559 | 0.1098 | 16.899 | <0.0001 | 2.8688 | 0.1267 | 22.649 | <0.0001 | |
| PF (V7)2 | 4.6183 | 2.6263 | 1.758 | 0.0794 | 2.7828 | 2.5932 | 1.073 | 0.2838 | |
| PF (V7)3 | 0.0964 | 0.1318 | 0.732 | 0.4645 | 0.0657 | 0.1402 | 0.468 | 0.64 | |
| PF (V7)4 | 0.1447 | 0.2335 | 0.62 | 0.5356 | 0.0664 | 0.2395 | 0.277 | 0.7819 | |
| CDH (V8)2 | -0.1292 | 0.0548 | -2.357 | 0.0188 | -0.1266 | 0.0622 | -2.036 | 0.0423 | |
| BM (V16)2 | 1.0748 | 0.2458 | 4.373 | <0.0001 | 1.5105 | 0.2282 | 6.619 | <0.0001 | |
| RX (x2) | 0.0226 | 0.0143 | 1.58 | 0.1148 | 0.0746 | 0.0189 | 3.943 | <0.0001 | |
| SHG (x12) | 0.0364 | 0.0152 | 2.402 | 0.0167 | 0.0278 | 0.017 | 1.64 | 0.1017 | |
| SZ (x13) | 0.0078 | 0.003 | 2.615 | 0.0092 | 0.0137 | 0.0031 | 4.46 | <0.0001 | |
| Sdate (y1) | 0.0003 | 0.0001 | 1.998 | 0.0463 | 0.0002 | 0.0001 | 1.44 | 0.1505 | |
| Dispersion | Constant | -0.6715 | 1.2585 | -0.534 | 0.5936 | -1.7272 | 1.2225 | -1.413 | 0.1583 |
| Stage (V1)2 | 1.5464 | 0.1938 | 7.98 | <0.0001 | 1.8895 | 0.1605 | 11.774 | <0.0001 | |
| CDH (V8)2 | 0.3707 | 0.1458 | 2.543 | 0.0113 | 0.0219 | 0.152 | 0.144 | 0.8856 | |
| BM (V16)2 | 0.7744 | 0.2225 | 3.48 | 0.0005 | 0.3142 | 0.222 | 1.415 | 0.1577 | |
| DBP (x10) | 0.1081 | 0.0534 | 2.026 | 0.0433 | 0.1696 | 0.0569 | 2.98 | 0.003 | |
| RX (x2) | 0.0787 | 0.0344 | 2.289 | 0.0225 | 0.1774 | 0.0373 | 4.762 | <0.0001 | |
| EKG (x11) | -0.0886 | 0.0388 | -2.282 | 0.0229 | -0.0904 | 0.0404 | -2.238 | 0.0257 | |
| SHG (x12) | -0.0913 | 0.0429 | -2.126 | 0.034 | -0.0502 | 0.0446 | -1.126 | 0.2607 | |
| SZ (x13) | 0.0104 | 0.0062 | 1.691 | 0.0915 | --- | --- | --- | --- | |
| SG (x14) | 0.115 | 0.0474 | 2.428 | 0.0155 | --- | --- | --- | --- | |
| Sdate (y1) | -0.0005 | 0.0003 | -1.63 | 0.1038 | -0.0001 | 0.0003 | -0.26 | 0.795 | |
| AIC | 1395 | 1582.087 | |||||||
Material and Methods
Materials
The study is based on a randomized clinical trial dataset of 474 PCPs having third or fourth stage PC. The source and contributor of the data set was D.P. Byar, and the analyses of this data set were given by Byar and his coauthors in, and it was well illustrated in the book by Andrews and Herzberg [19-21]. For each study unit, the following characteristics have been recorded:
1. Subject’s stage (=V1) (0=no cancer; 1=prostate cancer);
2. Estrogen (mg) (=RX=x2);
3. Months of follow up (=Dtime=x3);
4. Survival status (Alive=x4) (0=Alive; 1=Dead due to PC; 2=Dead due to heart or vascular; 3=Dead due to cerebrovascular; 4=Dead due to pulmonary embolism; 5=Dead due to other cancer; 6=Dead due to respiratory disease; 7=Dead due to other specific non-cancer; 8=Dead due to unspecified non-cancer; 9=Dead due to unknown cause);
5. Age(=x5);
6. Weight (=wt=x6);
7. Performance rating (=PF=V7) (0=normal activity; 1=confined to bed; 2=in bed <50% daytime; 3=in bed >50% daytime);
8. Cardiovascular disease history (=CDH=V8) (0=no, 1=yes);
9. Systolic blood pressure (=SBP=x9);
10. Diastolic blood pressure (=DBP=x10);
11. Electrocardiogram code(=EKG=(x11) (0=normal; 1=benign; 2=rhythmic disturb & electrolyte; 3=heart block or conduction; 4=heart strain; 5=old Myocardial Infarction (MI); 6=recent MI);
12. Serum hemoglobin (=SHG=x12);
13. Size of primary tumor (SZ=x13);
14. Index of tumor stage and histolic grade (=SG=x14);
15. Serum prostatic acid Phosphatase (=SPAP=y);
16. Bone metastases (=BM=V16) (0=no, 1=yes);
17. Date of study (Sdate=y1).
Note that there are some attribute characters and some continuous variables. In the present study, SPAP is treated as the dependent or response variable, and the rest others are treated as the explanatory or dependent factors/ variables.
Statistical Methods
The considered PC data are physiological, so the response or dependent variable SPAP is identified as heteroscedastic. Note that a heteroscedastic response is modeled by adopting stabilizing the variance, which is done by a suitable transformation, while it may not be always stabilized [22]. Here the response SPAP is an unequal variance continuous positive dependent variable, it can be suitably modeled by Joint Generalized Linear Models ( JGLMs) under gamma, or lognormal distribution [23, 24]. JGLMs under gamma, or lognormal distribution is well described in the books by Lee et al., and Das [23,25]. For ready application of these two models herein, they are shortly described as follows.
Log-normal distributed JGLMs
For the positive response Yi (=SPAP) with E(Yi=SPAP) =µi (mean) and Var (Yi=SPAP) =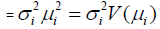 say, where σi2 ' s are dispersion parameters and V ( ) reveals the variance function, generally the log transformation Zi =log(Yi=SPAP) is
say, where σi2 ' s are dispersion parameters and V ( ) reveals the variance function, generally the log transformation Zi =log(Yi=SPAP) is
applied to stabilize the variance ,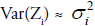 but the variance may not be stabilized always [22]. For deriving an improved model, JGLMs for the mean and dispersion are considered. For the response SPAP assuming log-normal distribution, JGL mean and dispersion models (with Zi =log(Yi=SPAP)) are as follows:
but the variance may not be stabilized always [22]. For deriving an improved model, JGLMs for the mean and dispersion are considered. For the response SPAP assuming log-normal distribution, JGL mean and dispersion models (with Zi =log(Yi=SPAP)) are as follows:
where 1 t x and 1 t g are the dependent or explanatory factors/ variables vectors linked to the regression coefficients β and γ, respectively
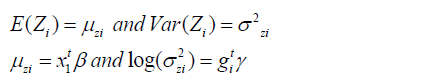
Gamma distributed JGLMs
For the above stated Yi’s (=SPAP), the variance has two components such as V(µi ) (based on the mean parameters) and (free of µi's). The variance function V (-) reveals the GLM family distributions. For example, if V(µ) = µ, it is Poisson, gamma if V(µ) = µ2, and normal if V(µ)=1 etc. Gamma JGLMs mean and dispersion models are as follows:
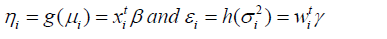
where g( )⋅ and h( )⋅ are the GLM link functions for the mean and dispersion linear predictors respectively, xitand wi t, are the dependent or explanatory factors/variables vectors linked to the mean and dispersion parameters respectively. Maximum Likelihood (ML) method is used for estimating mean parameters, while the restricted ML (REML) method is applied for estimating dispersion parameters, and these are illustrated in the book by Lee et al., [23].
STATISTICAL & GRAPHICAL ANALYSIS
The dependent variable SPAP is modeled on the rest sixteen explanatory factors/variables using JGLMs under both the gamma and the log-normal distributions. The best fitted model for SPAP is obtained based on the lowest Akaike Information Criterion (AIC) value that minimizes both the squared error loss and predicted additive errors [26]. Based on the AIC criterion, log-normal model fit (AIC=1395) of SPAP is better than gamma fit (AIC=1582.087). The final SPAP fitted log-normal and gamma JGLMs analysis results are displayed in Table 1. It is noted herein that two factors such as SZ & SG are used in the dispersion model of log-normal, while they are mixed with the other factors in the gamma fitted model. There is a lot of AIC difference between the log-normal and gamma models. Number of explanatory factors in the log-normal model is more than the gamma model, yet the AIC of the log-normal model is smaller than the gamma model. In epidemiology, partially significant effects are considered as confounders. For better fitting, some confounders or partially significant effects such as PF, RX (in the mean model), and SZ, Sdate (in the dispersion model) are included herein (Table 1) [26].
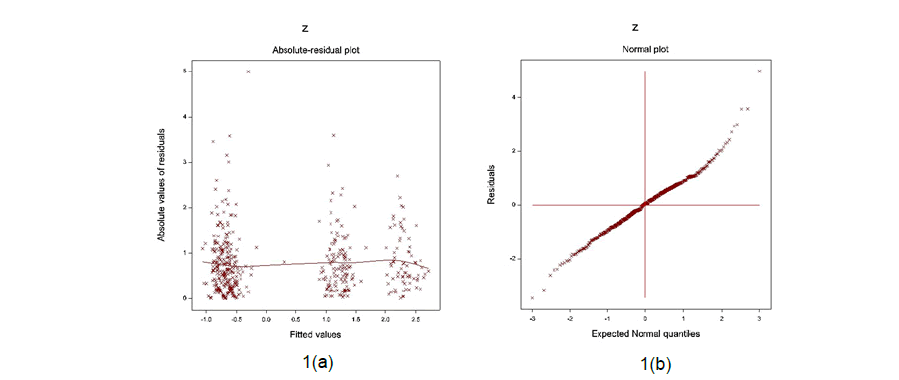
The data generated SPAP models are examined by graphical diagnostic tools. The best fitted log-normal SPAP JGLMs (Table 1) are diagnosed in Figure 1. Figure 1(a) reveals the absolute SPAP log-normal JGL fitted residuals plot against its predicted values, which is exactly a flat straight line, concluding that variance is equal with the running means. Figure 1(b) shows the SPAP lognormal fitted mean model (in Table 1) normal probability plot, which does not show any fitting discrepancy. Therefore, both the Figures 1(a) & 1(b) indicate that the SPAP log-normal fitted JGLMs are nearly close to the unknown true SPAP models.
Figure 1: For the JGL log-normal SPAP fit (Table 1), the 1(a) absolute residuals plot against the SPAP fitted values, and 1(b) the normal probability plot for the SPAP mean model
Results
In Table 1, the summarized SPAP analysis outcomes for both JGLMs are displayed. In the article, the log-normal fitted analysis outcomes are discussed herein. From the derived results in the lognormal fitted mean model (Table 1), it is shown that mean SPAP level is positively linked with PCPs (P<0.0001) and PCPs confined to bed (P=0.0794). Mean SPAP level is positively connected to PCPs with BM (P<0.0001), while it is negatively connected to CDHPs (P=0.0188). In addition, mean SPAP level is positively related with SHG (P=0.0167), estrogen (RX) (P=0.1148) (in log-normal model, but in the gamma model P<0.0001), size of primary tumor (P=0.0092) and study time (P=0.0463). Variance of SPAP level is positively connected to PCPs (P<0.0001), PCPs with BM (P=0.0005), and CDHPs (P=0.0113). Also, variance of SPAP level is positively related with DBP (P=0.0433), estrogen level (P=0.0225), size of primary tumor (P=0.0915) and index of tumor stage and histolic grade (P=0.0155), while it is negatively connected with Electrocardiogram Status (EKG) (P=0.0229) and SHG (P=0.0340).
JGL log-normal fitted mean model (Table 1) is estimated log(SPAP)=-2.0284+1.8559 Stage2 +4.6183PF2 +0.0964 PF3 + 0.1447 PF4 -0.1292CDH2 +1.0748 BM2 +0.0226 RX + 0.0364 SHG+0.0078 SZ+0.0003 Sdate, and the JGL log-normal fitted SPAP dispersion (σˆ 2 ) model (from Table 1) is σˆ 2 =exp(-0.6715 +1.5464 Stage2 +0.3707 CDH2 +0.7744 BM2 +0.1081 DBP +0.0787 RX --0.0886 EKG -0.0913 SHG+0.0104 SZ+ 0.1150SG-0.0005 Sdate).
Discussions
From the derived JGL log-normal fitted SPAP analysis findings (Table 1) and the above SPAP’s mean and dispersion models, the following can be illustrated directly. Mean SPAP level is positively linked with PCPs (P<0.0001) (0=no cancer; 1=prostate cancer) and PCPs confined to bed (P=0.0794) (0=normal activity; 1=confined to bed; 2=in bed <50% daytime; 3=in bed >50% daytime). These indicate that SPAP level is higher for PCPs and also for PCPs confined to bed than normal. Th ese su pport th e earlier results [1, 2, 7-9, 11-13, 16, 17]. In addition, mean SPAP level is positively connected to PCPs with BM (P<0.0001) (0=no, 1=yes), concluding that SPAP level is higher for PCPs with BM than normal. These above three findings are directly related with PCPs at their different stages. In the earlier articles, these findings were not derived using stochastic modeling. These were concluded based on percentage readings [1, 2, 7-9, 11-13, 16, 17]. Therefore, SPAP is considered as a biomarker for PC.
Beside these above direct effects on PCPs, SPAP has many effects on the other biochemical and clinical disease history factors. Mean SPAP level is negatively connected to CDHPs (P=0.0188) (0=no, 1=yes), concluding that SPAP level is higher for the subjects with no CDH. This is not definitely specified in any previous articles [1,4,9-13,15]. Mean SPAP level is positively related with SHG (P=0.0167), concluding that it rises as SHG level increases. Mean SPAP level is positively related with estrogen (RX) (P=0.1148) (partially significant), implying that it rises as RX increases. Also, mean SPAP level is positively related with the size of primary tumor (P=0.0092) and study time (P=0.0463), concluding that its mean level increases with the increase of the size of primary tumor and study time. Best of our knowledge, these findings are not pointed out in any previous articles
From the log-normal SPAP fitted dispersion model (Table 1),it is shown that variance of SPAP level is positively connected to PCPs (P<0.0001), PCPs with BM (P=0.0005), and CDHPs (P=0.0113), interpreting that SPAP levels are higher scattered for PCPs, PCPs with BM, CDHPs, then normal. In the mean model, it has been established that SPAP level is positively connected to PCPs and PCPs with BM, which are heterogeneous populations. Therefore, the dispersion of SPAP levels are highly scattered. Also, variance of SPAP level is positively related with DBP (P=0.0433), RX (P=0.0225), size of primary tumor (SZ) (P=0.0915) and index of tumor stage and histolic grade (SG) (P=0.0155), concluding that variance of SPAP level is increasing with the increase of DBP, or RX, or SZ, or SG. In addition, the variance of SPAP level is negatively connected with Electrocardiogram Status (EKG) (P=0.0229) and SHG (P=0.0340), implying that it increases with the decrease of EKG, or SHG level. Best of our knowledge, the above findings related to the dispersion of SPAP levels are not developed in any earlier articles.
The derived outcomes of the current article related to the associations of SPAP with other factors, or variables for the mean and dispersion models are discussed above. Some of the outcomes such as mean SPAP levels are higher for PCPs and PCPS with BM are pointed in the earlier articles, but the other outcomes of the current article are very little stated in the previous articles [1, 3, 6, 9-12, 14]. The report supports the previous known outcomes. But the other outcomes of the report are completely new in the prostate cancer literature. So, these are not compared with the previous outcomes. The article has focused on several associations of SPAP with many factors or variables both in the mean and dispersion models, which are not focused in any earlier articles. One can verify the present associations of SPAP using the data as stated in the materials section
Conclusion
The relationships of SPAP with physical, anatomical, biochemical, clinical history of diseases of the subjects are focused in the current article based on probabilistic or stochastic modeling. The best model is obtained based on the graphical diagnosis, comparison of two distributions, lowest AIC, and the small standard error of the estimates. All the derived results are focused herein based on the selected best model. The derived results support all the known earlier findings, but there are many results, which are not known in the earlier literature. Exactly similar findings can be obtained from any such similar data, even though the current study is based on a very old data set. Note that the medical data set is physiological data, which do not change over time for the similar group of study subjects. So, the term ‘old and new’ data set in case of physiological data is invalid. The report focuses on many new findings in the prostate cancer literature, which may be very helpful to the researchers, medical practitioners, and common men. It concludes that SPAP is highly associated with PCPs and along with their many factors such as SHG, estrogen level, BM, size of primary tumor, DBP etc. Higher SPAP level of a man always indicates prostate cancer along with many hidden facts of the subjects. Care must be taken of SPAP level at older ages of men.
Conflict of Interest
The author confirms that this article content has no conflict of interest.
Acknowledgement
The authors are very grateful to the principal data investigators D.P. Byar (National Cancer Institute), who provided the data freely for scientific study.
References
- Hsing AW, Chokkalingam AP. Prostate cancer epidemiology. Front. Biosci. -Landmark. 2006; 11:1388-1413.[Google Scholar] [CrossRef]
- Kong HY, Byun J. Emerging roles of human prostatic acid phosphatase. Biomol ther. 2013;21:10.[Google Scholar] [CrossRef]
- Kong HY, Byun J. Emerging roles of human prostatic acid phosphatase. Biomol ther. 2013;21:10.[Google Scholar] [CrossRef]
- Hobisch A, Eder IE, Putz T, Horninger W, Bartsch G, et al. Interleukin-6 regulates prostate-specific protein expression in prostate carcinoma cells by activation of the androgen receptor. Cancer res. 1998;58:4640-4645.[Google Scholar]
- Bussemakers MJ, Van Bokhoven A, Verhaegh GW, Smit FP, Karthaus HF, et al. DD3:: A new prostate-specific gene, highly overexpressed in prostate cancer. Cancer research. 1999;59:5975-5979.[Google Scholar]
- Gupta A, Lotan Y, Ashfaq R, Roehrborn CG, Raj GV, et al. Predictive value of the differential expression of the urokinase plasminogen activation axis in radical prostatectomy patients. Eur Urol. 2009;55:1124-1134.[Google Scholar] [CrossRef]
- Madu CO, Lu Y. Novel diagnostic biomarkers for prostate cancer. J Cancer. 2010;1:150.[Google Scholar] [CrossRef]
- Batta A, Panag KM, Singh J. Diagnosis of prostate cancer-Role of biomarkers. Int J Cur Biomed Phar Res. 2012;2:339-345.[Google Scholar]
- Gutman AB, Gutman EB. An “acid” phosphatase occurring in the serum of patients with metastasizing carcinoma of the prostate gland. J clin investig.1938;17:473-478.[Google Scholar] [CrossRef]
- Small EJ, Schellhammer PF, Higano CS, Redfern CH, Nemunaitis JJ, et al. Placebo-controlled phase III trial of immunologic therapy with sipuleucel-T (APC8015) in patients with metastatic, asymptomatic hormone refractory prostate cancer. J Clin Oncol. 2006;24:3089-3094.[Google Scholar] [CrossRef]
- Sheridan T, Herawi M, Epstein JI, Illei PB. The role of P501S and PSA in the diagnosis of metastatic adenocarcinoma of the prostate. Am. j. surg. pathol. 2007;31:1351-1355.[Google Scholar] [CrossRef]
- Veeramani S, Yuan TC, Chen SJ, Lin FF, Petersen JE, et al. Cellular prostatic acid phosphatase: a protein tyrosine phosphatase involved in androgen-independent proliferation of prostate cancer. Endocr-Relat Cancer. 2005;12:805-22.[Google Scholar] [CrossRef]
- Xu H, Wang F, Li H, Ji J, Cao Z, et al. Prostatic acid phosphatase (PAP) predicts prostate cancer progress in a population-based study: The renewal of PAP?. Dis Markers. 2019;2019.[Google Scholar] [CrossRef]
- Kirschenbaum A, Izadmehr S, Yao S, O’Connor-Chapman KL, Huang A, et al. Prostatic acid phosphatase alters the RANKL/OPG system and induces osteoblastic prostate cancer bone metastases. Endocrinology. 2016; 157:4526-33.[Google Scholar] [CrossRef]
- Balakrishna SV, GK VG, Ganesh V. A study of serum levels of prostate specific antigen, prostate acid phosphatase in prostate cancer patients and its complications on liver. Int Surg J.2021; 8:554-548.[Google Scholar] [CrossRef]
- Vickers AJ. Prostate cancer screening: time to question how to optimize the ratio of benefits and harms. Ann Intern Med. 2017; 167:509-510.[Google Scholar] [CrossRef]
- Ostrowski Ws, Kuciel R, Bem S. Characterization of human prostatic acid phosphatase and its clinical significance. J Clin Biochem Nutr.2000;28:233-244.[Google Scholar] [CrossRef]
- Mandiramoorthy SK. To identify novel oncogenes for the design of novel tools for diagnosis and treatment of cancer.[Google Scholar]
- Byar DP, Corle DK. Selecting optimal treatment in clinical trials using covariate information. J Chronic Dis. 1977;30:445-459.[Google Scholar] [CrossRef]
- Byar DP, Green SB. The choice of treatment for cancer patients based on covariate information. Bulletin du Cancer. 1980;67:477-490.[Google Scholar]
- Andrews DF, Herzberg AM. Data: a collection of problems from many fields for the student and research worker. Springer Sci Bus Media. 2012.[Google Scholar]
- Myers RH, Montgomery DC, Vining GG, Robinson TJ. Generalized linear models: with applications in engineering and the sciences. John Wiley Sons; 2012.[Google Scholar]
- Lee Y, Nelder JA, Pawitan Y. Generalized linear models with random effects: unified analysis via H-likelihood. Chapman Hall/CRC; 2018.[Google Scholar] [CrossRef]
- Das RN, Lee Y. Log-normal versus gamma models for analyzing data from quality-improvement experiments. Qual Eng. 2008;21:79-87.[Google Scholar] [CrossRef]
- Das RN. Robust response surfaces, regression, and positive data analyses. CRC Press.2014.[Google Scholar]
- Hastie T, Tibshirani R, Friedman JH, Friedman JH. The elements of statistical learning: data mining, inference, and prediction. N Y: Springer;2009.[Google Scholar][CrossRef]